Time complexity in data structure and algorithms (DSA) refers to the computational complexity that measures the amount of time an algorithm takes to complete as a function of the length of its input. Here are examples of algorithms with constant, linear, logarithmic, and exponential time complexities implemented in Python:
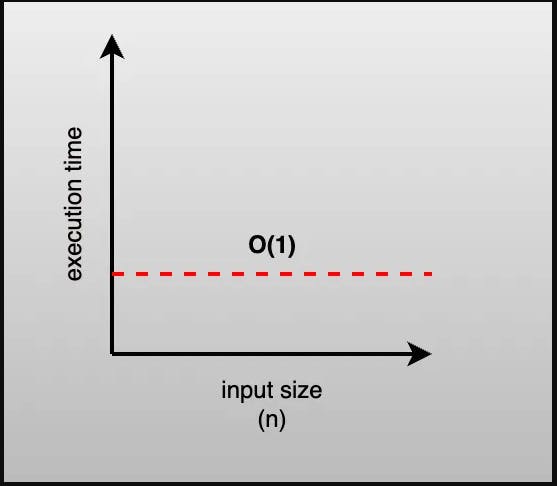
Constant Time Complexity (O(1)):
Algorithms with constant time complexity execute in the same amount of time regardless of the size of the input data.
Example:
def constant_algo(items):
print(items[0])
# No matter the size of items, this function always prints the first element.
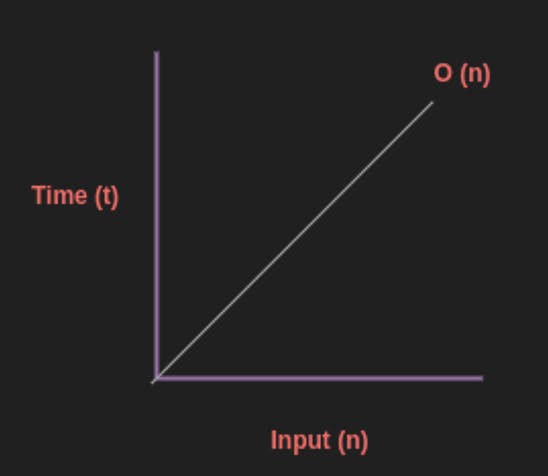
Linear Time Complexity (O(n)):
Algorithms with linear time complexity have their execution time directly proportional to the size of the input data.
Example:
def linear_algo(items):
for item in items:
print(item)
# The time taken to print each item increases linearly with the size of items.
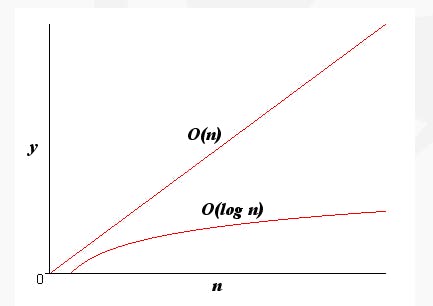
Logarithmic Time Complexity (O(log n)):
Algorithms with logarithmic time complexity typically halve the input data size at each step.
Example: Binary search algorithm
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
# In each iteration, the size of the input (arr) is halved, leading to logarithmic time complexity.
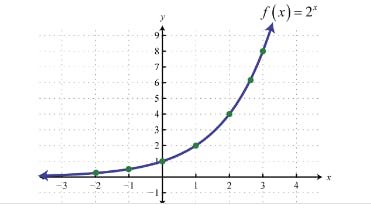
Exponential Time Complexity (O(2^n)):
Algorithms with exponential time complexity grow very rapidly with the increase in input size.
Example: Recursive Fibonacci series calculation
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
# Each call branches into two more calls, resulting in an exponential growth in time complexity.